Nice Deagle at 1:29 *eye roll*


As far as i’m concerned, Sons Of Guns is setting how firearm enthusiasts are viewed, back decades. I’ve only see a couple of episodes, and I’m not an angry person but I really wanted to smash my TV numerous times while watching.
Classic move to just switch the gun out but pretend you’re still using it. Discovery FAIL!
Discovery actually had this clip up on their site, but someone called them on their bullshit so they pulled it.
Stephanie Hayden (the Derptress herself) confronted on facebook about the incident:
Hat tip: ozwald & JWhite



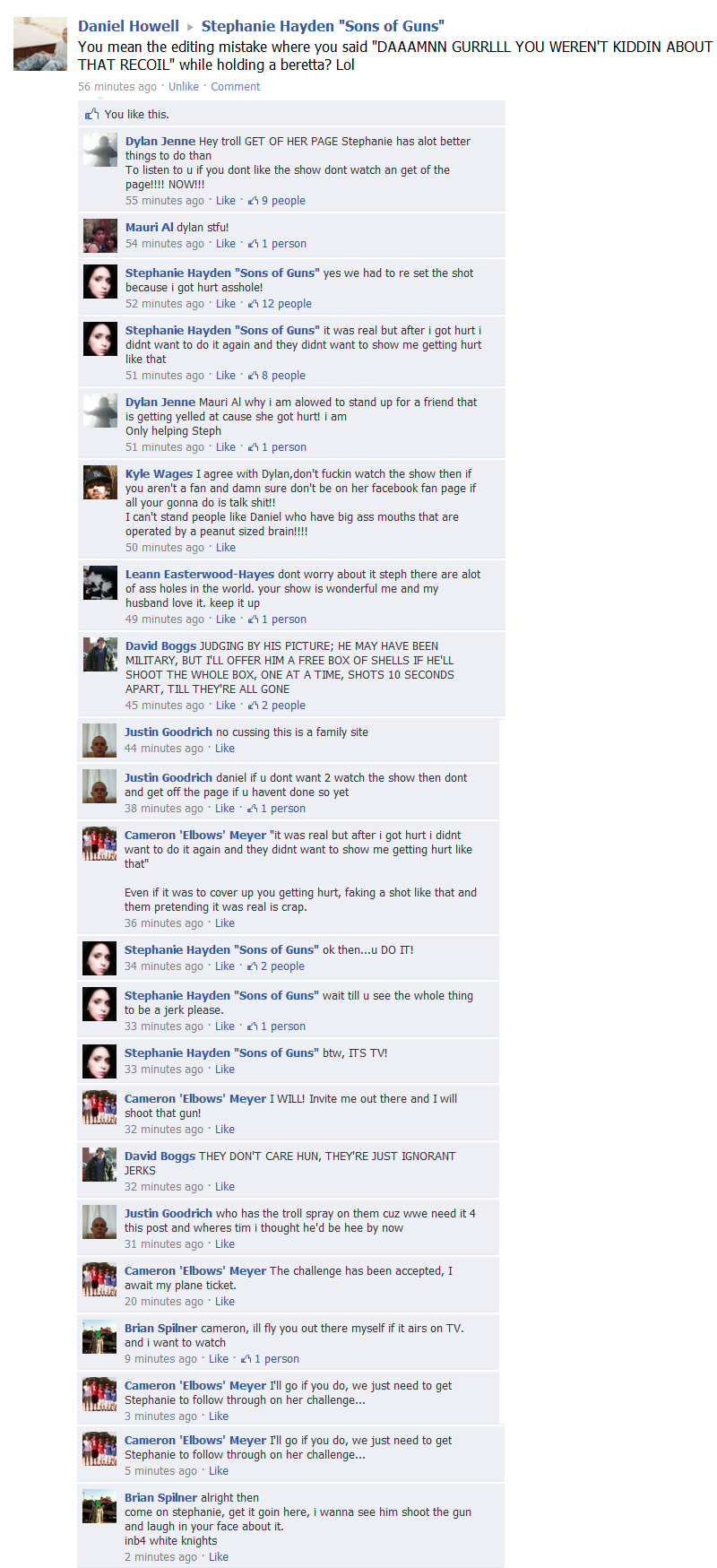
Comments
95 responses to “Sons Of Guns Derptastic Deagle Episode”
There was an episode from Season One where they had to make some kind of blank-firing movie prop gun or similar, and the promo for the episode had the owner shooting it off inside the shop.
Two words: Brandon Lee. Three words: Jon-Eric Hexum.
That’s when i dropped the season pass from my TiVo and I’ve not watched it since. These aren’t gun owners I’m around all the time, that’s for sure.
I really do hate this show. But again, they cater to a totally different market than the one I inhabit. I don’t have money to throw away on overpriced Saiga conversions and useless modifications. Their customers, obviously, do.
it’s a magical baretta 92, hahahahaha..
I laughed when I saw this video :))
She has a touch of the Down’s me thinks…
Yea, and I hear her favorite band is “Syndrome Of A Down”
hahahaha.. #derp#
@ 1:12 she says “I like handguns that go boom”. Well, now her reputation has gone BOOM to match. I hope she likes that too.
lol thats classic editing at its best :)
I really honest to god want to cry now. This totally wrecked my night. I have to lay down now.
Oh my god she’s gotten SO fat and overly emotional. I’m beginning to think she’s really a man O.o
haaaahaaa ultra mega epic FAIL!!!
I watched in horror last week as the shop owner was handling a UZI and muzzle-swept 3 people at least half a dozen times while showing off mods. For a ex-Marine and long time shooter, his lack of the most basic safety principle was a letdown. This only adds to the fiction.
Was the gun loaded? I doubt it would be if they were showing it off inside the store.
Being safe is one thing, but when you start to think that guns are just like what the Brady Campaign and such think they are (able to kill all the time just by looking at them the wrong way) then there’s a bit of a problem. If the man personally cleared his gun, let him do as he wishes.
Safety has nothing to do with the brady campaign. “If the man personally cleared his gun, let him do as he wishes.”???
You must be a very trusting person, putting your life in the hands of every Tom, Dick, and Harry that has the ability to buy, steal, or find a gun. Expecting the gun to be unloaded just because the person holding it says it is is a great way to get dead.
As they say, loaded guns shoot bad guys, unloaded guns shoot friends.
I’ll continue jumping out of the way of “unloaded” guns and explaining that I get defensive when strangers point guns at me. You are welcome to stand there until an accident happens.
If everyone that gets swept has been shown that the weapon is clear, there is no problem.
The switcheroo with the Beretta and the appalling acting are incredibly lame. Wonder if the footage gets left in the actual episode?
If he cleared his gun let him do as he wishes????What diluted logic is that? No offense, but thats what happens time and time again when someone says: “its not loaded” and cranked off a ND. Bad safety habits will carry over to the range, even from the shop. You work with guns all day, I get that part, but you also have a responsibility now as millions of people are watching your actions. Be a representative of responsible ownership. IMO, no one gets a free pass on muzzle sweeps.
Acting like the gun is loaded at all times is good.
However, think of the context. For example, YouTube videos, where the person points a gun at the camera while speaking about it. It’s implied that the camera is likely mounted somewhere at chest height, so he’s point the gun at himself.
Chances are he’s unloaded the gun and cleared the chamber. It is entirely safe.
The same thing in a gun store. No gun is going to be locked and loaded, or even LOADED in a gun store. While yes, constant muzzle sweeping all the time is a bad thing, but when it’s safe, and you need to sweep to SHOW OFF PARTS OF THE GUN, jumping down their throat isn’t all that nice.
tl;dr safety is good, context is better.
I’ll take safety over context, luck and trust any day.
You must really have a fit when you watch action movies.
Correction:
I’ll take Chuck Norris over safety, context, luck and trust any day.
“Was the gun loaded? I doubt it would be if they were showing it off inside the store.”
When I was in class for my concealed carry, the instructor, who ran the local gun shop, told us this story:
A few months prior, they had ordered some expensive and highly detailed lever-action rifle for a customer (I don’t remember the make and model off the top of my head at the moment). He had just gotten it in fresh from the factory and unpacked it when a customer came in. He set it aside to tend to the customer. Someone else in the store asked to take a look at it. The guy cocked the lever, and . . . a round popped out.
The owner immediately called the company to tell them what happened. Apparently, before they’re shipped, they have an automated system that lines up several of the weapons and automatically fires and cycles 5 rounds through them. Apparently, on this batch, only 4 rounds were fired. There were others on their way to stores with a live round in the chamber.
Just because it’s in a store, doesn’t mean someone, somewhere along the line, hasn’t screwed up and loaded the weapon.
I’m glad I’m not the only one that thinks this show is ridiculous. I love you guys.
stocks on pistols are lame *runs and hides*
BANNED FOR LIFE! haha just kidding.
a stock for a Glock? it has never been done before! we’re gonna open up a whole new market!
LOL
Why modify the deagle..how bout stop shooting it if you’re too teenie to shoot it. It’s not like it’s a real gun..it’s a friggen toy that has no practical use. It’s a novelty so you can show your friends that you have a 50 “like the one on tv!” There’s plenty of sexist gun dealers that’ll put a 32acp revolver in her hands.
Im with ya, she could sell the Deagle and buy 2 or three good semi autos (Springfield, Glock, whatever..)
What’s wrong with modifying a gun so that you can shoot it comfortably? And novelty nothing, it’s the perfect self defence weapon. I mean, if you tried to steal her purse, and saw her pulling out a Desert eagle (With a stock lol), would you just drop it and run or face that down like an idiot? :/
Now that’s badass! I want a shapeshifting gun now too!
I don’t care, the Desert Eagle is still “The bacon of pistols”
Yeah, and the 92 the “bologna of pistols”.
And the Glock the “Great value” brand of pistols :3
And Hi-Point is the “McDonalds” of pistols.
Hi point doesn’t get one because it’s so cheap lol
I was gonna say Hi-Point doesnt get one because we dont support inappropriate uses of firearms… LOL. “Guns dont go in the gutter son!”
Hi-Point is the Spam of pistols..scratch that it’s the Treat of pistols.
She might like, “guns that go boom” but she is obviously not a shooter.
She was closing her eyes and anticipating recoil before shooting the 92.
I can see I’m not missing anything positive by not watching this show.
Ohh but come on. They revolutionized the tactical community by mounting a shotgun under a “m16”. Oh, wait, never mind.
Why do they even bother to let her shoot? The desert eagle obviously isn’t designed for people who aren’t already lumberjacks in frame and size. What kind of morons are they dealing with? On Top Shot when the women were shooting the S&W 500, even those women had trouble with the recoil and they’re “professional” shooters (according to the History Channel).
To be fair, from interviews, it would appear as though the folks at Red Jacket do not have a whole lot of control over what Discovery airs or how they do it.
However (and this is a big “but”), that was damned stupid.
the hilarity continues of facebook
http://i.imgur.com/SlBTj.png
Thanks ozwald, I added that to the end of the post!
If you like the show or not, if Discovery FUBAR’s it up or not, it amazes me how quickly gun guys are to turn on their own and cannibalize each other. While I face palm from time to time over Sons-of-Guns too, I am just glad that the gun world is getting more and more exposure. Top Shot included as well. If people get into this show and buy or vote pro-gun because if it, then I am all for it.
Even though I don’t like Top Douchebag, I agree at least it portrays shooting in a positive responsible light. Sons of guns in my opinion however does the opposite.
The reason this show pisses me off is I can’t imagine it doing anything but making guns LESS attractive to the general population. “THIS is how gun owners think and act? Wow… I had no idea.. I don’t want to be associated with them then.” This isn’t ‘turning on our own’ when it makes us ALL look like the unwashed hordes the elitist left describe us to be. To be honest I personally have a problem with the way a lot of gun lovers carry themselves publicly and politically. If this show upsets ME just IMAGINE what it’s doing to the average person.
I blame the entertainment business model that wants their program to be, “edgy,” or, “cool.” The theory is that this draws in a larger demograph which translates to more dollar signs. You see this in movie properties all the time when the source material is butchered to cater to the general public (see sequels of popular R rated franchises that go PG13 for example). I don’t agree with this practice at all.
HEY LADY, IF YOU DON’T LIKE THE RECOIL AND AWKWARDNESS OF THE DEAGLE BUY ANOTHER HANDGUN!!!!!!!! SERIOUSLY, DON’T WASTE YOUR MONEY ON STUPID-ASS MODS!!!
I MEAN GODAMMIT WHY’D YOU EVEN BUY IT IN THE FIRST PLACE!?!?!?!?
Don’t like the people on the show (blowhards), don’t like the fake jobs they work on (water-cooled dual M16s? no government agency commissioned that), don’t like the image they convey of gun owners (machineguns, grenade launchers? who needs paperwork!).
All the lame drama of Slop Shot with none of the safety or responsibility.
After giving each program a chance, I refuse to watch either show.
I actually like the show. Is it a show for purist shooters? No way! It’s all sizzle and very little steak. It’s the difference between playing NBA Jam (yes I’m dating myself here) vs. playing some HORSE, with a real ball, in your driveway with a buddy.
If you take the show as a “wahoo” kind of program it’s great. So what if a bunch of people see the show and spend their hard earned cash on “tactical” Saiga 12s, Deagles, or 7.5″ AR SBRs? So what if they never learn proper sight alignment, how to hit something with a rifle beyond 25 yards, any safety procedures, uh…wait a second…yeah that might be a problem :).
I actually enjoy the show. They make some interesting stuff…but that is really cheap of them to deceive viewers like that. Especially so blatantly. LOL at the whiteknights on facebook. When will guys learn.
Here’s my two cents and if you don’t agree with it that’s cool, just an opinion…
The show is a good thing for gun enthusiasts. The reason is it’s showing that guns can be safely handled, shot modified and there’s some very interesting people doing it. Regardless of what us “GUN OWNERS” see as BS, or slight of hand or not exactly something we would do… others who may not own a gun, nor belong to the NRA or even thought of getting one, may decide to get one and get training and learn… IF it grabs 10 people a week into NRA it’s a great show IMO. We need more gun owners active in the fight to keep our rights. These guys are putting on a show, it’s not geared to those of us WHO KNOW ABOUT GUNS. it’s geared to the average joe…
I know there’s those that will say we don’t need any folks that would buy this BS or whatever.. Fact is we need a united front to stop the slide into total government control of our rights…There’s how many gun owners? How many are active in fighting to keep our rights? We need to fight and if this show helps in anyway I’m a supporter…
1. Is the show still good if it portrays gun owners as dangerous and irresponsible to the general public?
2. Is this show actually creating gun supporters, or is it really creating gun opponents?
3. If gun supporting people do not support the show based on its portrayal of gun owners/lovers, how do you expect the general population to receive it?
Obviously it’s doing pretty well… It’s still on and it’s got a very big audience. A lot of shows show folks doing things not exactly safe, hunting shows for example… Now some of us holier than thou gun owners may see every little thing not done right, but I assure you MOST gun owners don’t watch the show for a safety lesson or a class on building a master key… It’s entertainment and it’s a business look inside that’s it… Kind of like thinking all the folks watching Jersey Shore are gonna run out and get spray on tans and fake tits… I think when we bash a show like like this, WE do more harm to our own than the show does… But carry on.
Think about how Jersey Shore makes Italian Americans/Jersians look to the general population, then apply that same thinking to gun owners through sons of guns. If you need a little help, heres the south park episode relating to Jersey Shore.
http://www.southparkstudios.com/full-episodes/s14e09-its-a-jersey-thing#
I cant wait to see the sons of guns episode….
Sons of Guns is a joke. The folks on Swamp People handle firearms better than these derps.
I stopped watching after the first episode I ever watched, where they bastardized that Thompson and turned it tacti-cool. Even if it was a Semi-Auto replica, I couldn’t even finish watching. I’m glad I haven’t been keeping up with it, especially if this is whats been going down.
But that Thompson was cool. Imagine a horde of soldiers carrying modernized those. If we can do it to a grease-gun, why cant we do it to a Thompson? I’d do it. Screw you purists, i’ve got a Thompson with a flashlight, a scope off of a sniper rifle, a laser and a masterkey. I AM INDIFFERENT TO YOUR OPINION ON MY FIREARM. Dont be jelly just because i can afford to bastardize one and you cant.
Do you have a pack mule to carry it? The Thompson itself weighs something like 74 pounds.
Don’t you need paperwork for putting a stock on a handgun?
I’m pretty sure that qualifies it as an SBR…
Jake, THANK YOU!!
That was my first question after watching that vid.
Followed up quickly with “why don’t they just sell her a $300 Mossberg 500 for home defense??”
As cool as it might see as a fun safe queen / range toy, they’re proposing a destructive, expensive, and DERPTACULAR solution to a problem which largely exists with the user. It makes me wonder if that “build” is a complete and utter setup for TV.
I was hoping they would say something like turning your pistol into an SBR would be cool, but we’ll ahve to jump through some dumb hoops with BATFE.
They also could have converted it to a milder caliber or added a brake. I think I’ve seen Deagles with a second slide (and mag?) to swap calibers and brake would add some more boom so that’s a toofer.
The purpose of that modification was to sell it, of course.
It is a business, and the mark walked right on in to the carnival…
Or, more likely, the producers sat down and thought that making a shoulder stocked Deagle would be kewl and put the mark up to it.
http://i51.tinypic.com/2ilc9jb.jpg
Ha! They thought they could slip that one by! At a passing glance the beretta (almost) passes because of the open slide design also found on the DE. But to anyone who knows anything about guns, its clearly a 9mm berettta, and not the big bad monster Desert Eagle in her hands!
Discovery, and Red Jacket better polish up the act a bit before they alienate their audience with bad editing! (Even the clueless couch potatos who have never picked up a weapon in their life, which I’m sure accounts for better than 70% of their audience)
EPIC FAIL!!!
I’ve seen parts of a couple episodes of this show; I can’t really stand it. Everything’s so over-the-top, they just look like a bunch of dumb rednecks who are good at working on guns.
Yeah definitely over the top.
Here’s some (imagined) future shows:
Suppressed 155mm Howitzer
Belt Fed Gatling 12g shotgun for a one armed combat wounded vet to hunt ducks
Get a bunch of yahoos together for a full-auto shootoff and hit old cars filled with Tannerite (wait that’s pretty much every show).
Invite 50 Cent on to the show and create an AK with an iPod in the stock, all the metal is gold plated with rhinestones.
I’m hoping for a taser or stungun attached to the rail of a handgun.
Lawsuit waiting to happen.
About that Howitzer suppressor….
http://img220.imageshack.us/img220/7751/germancannonmuffler04ak3.jpg
Here’s a better view of one: http://www.thefirearmblog.com/blog/2009/10/16/worlds-largest-gun-suppressor/
Also, my little sister, who is 18 years old and smaller than this dweeb, shot a .50AE Desert Eagle just fine a couple years ago. And a Smith and Wesson M29 with a 3 inch barrel, which I found to kick a lot harder than the Desert Eagle, with no problems. She has had no training other than some quick advice from myself.
Long story short, Ms. Haden is a wimp… it’s not that hard to shoot one of these and not hurt yourself.
Well, everyone knows TV is a lot of fakery. But then she gets all defensive about it on facebook, which is pretty stupid.
because shes a child.
Found a site with the video… Looks like they pulled all the Youtube videos.
http://www.videozula.com/video/evhhqk-sons-of-guns-desert-eagle-monster.html
@1:19 – Deagle Sauce
@1:24 – Italian Sauce
Yeah. I just had a convo about Sons of Guns with some coworkers and they seemed to think they are some “hot shit” professionals. I’ve watched the show. Its the same useless crap as you mentioned. Man portable M1919 for a “competition”? BS… And then the stand ins who pretend to be friends of the show or whatever. Like the old lady with a “deagle” what? I honestly dont see her shooting that thing ever. It looks brand freaking new. The only people I see shooting an IMI Desert Eagle .50 are Counterstrike nerds at the local range. “Boom, yeah, heh heh, that was a head shot dude… Oh word! This is just like on D-Dust2 my favorite map yo. You gotta try it! I wonder if they have an AWP”
Personally… I’ve avoided being “that guy” by renting that gun at the range. I’m willing to bet the .50AE has a little bit more kick than a .45ACP or .44 Magnum, both which I have shot.
FPS russian shoots it one handed.
http://www.youtube.com/watch?v=-haq8I72DxA
Thanks! Hahahah Discovery is hilarious. I updated the embeded vid in the post.
I liked the History and Discovery channels a lot more when they were about history and science rather than Ice Road Trucking, Hillbillies building absurd guns, Swamp Logging, etc., etc.
Grandpa knows what’s what. The History Channel was awesome when 80% of it’s programming was about weapons and war and science. Not syfy channel crap like UFO hunters, Bravo crap like Ice road truckers, and the Outdoors Network crap like Top Shot. American top gear was fine though.
Hell, the day they took Mail call of the air it got worserer. And then when they took Gunney out of History channel entirely, eeeeverything went to shit :C
+1 for the Gunny. And yeah, when they actually showed HISTORY on the History channel it was pretty nice. Coming from a military family, I watched quite a few of those WW2 and Vietnam documentaries with my parents, and actually enjoyed learning something instead of watching Ms. Derpette here fail at firearms.
+1
Taser mounted to a M4? An engineering marvel and lawsuit waiting to happen. This is making legitimate gunowners and gunsmiths look bad.
http://defense-update.com/images/TASER-rail.jpg
The article that picture’s from is several years old. I haven’t seen any pictures of soldiers with this setup.
http://defense-update.com/products/t/taser.htm
As if it wasn’t retarded enough that the lady bought a gun she couldn’t handle (try something more your size foolish woman) then the gun shop girl wants to shoot it, can’t handle it and hurts herself *doh! but instead of airing that she couldn’t handle the pistol they try to pass off a beretta on us. AS A DESERT EAGLE. Don’t even have to be a gun nut to tell the difference between those two.
This show constantly boggles my mind with stupidity. RULE 1 OF FIREARM SAFETY: always treat a weapon as if it was loaded, never point it at something unless you intend to destroy it. NO MATTER WHAT. And to all these IDIOTS that wrote in the comments that shit is no big deal, it is. As former army I’ll tell u right now, you muzzle sweep me, I WILL KILL YOU. Never, ever point a gun at me, or anyone else, it IS that serious. unloaded, loaded, full of blanks, doesn’t matter. Follow that rule always. Stupidity begets stupidity. I never want to hang around you careless callous gun owners, and i definitely don’t want to be around, or watch, this show for its eternal carelessness with gun safety.
So if someone on tv muzzle sweeps you are you going to kill them? Or is it just people close by you kill for muzzle sweeping you? I bet gunshows are a real killing field for you.
Congrats on being a bigger idiot than those you are calling idiots.
Agree. I almost pulled my side arm at a gun range to shoot a man who was sweeping my wife and I with a AK-47. About the third time, I told him, “You point that gun at me and my wife again, I will shoot you.” He didnt even realize he was doing it. He had bought a brand new gun and had no clue about safety or range protocol. He didnt even apologize, he simply looked at me and life like it was a joke.
And I am like you, I wouldnt hesitate to shoot someone pointing a gun at me, accidental or not.
Hey this is gonna be off topic but why hasn’t anyone thought to fabricate a damn muzzlebreak for it? You’ll still get flip and rise with a stock by itself.
if i still had a tv, this show would cause me to ‘elvis’ it in no time.
Yeah as I read these comments about “muzzle sweeps” I thought about how I guess most of these guys must not go to gun shows because everyone in there is “muzzle sweeping” everyone else. Don’t get me wrong, I’m am super anal about gun safety, personally and I damn sure don’t want any gun pointed at me, even if I cleared myself. I do enjoy watching the show tho because I love watching guys blow shit up. It’s TV folks, calm down…
The episode with the muzzle sweep and done with a gun that was modified to only shoot blanks. A live round of ammunition couldn’t even be put into the gun and Will stated that even though that is thes case it should never be done.
Anyone notice how discovery pulled the clips on youtube, and edited the show on TV to no longer show the Beretta? I was channel surfing last week and saw the deagle and stopped for the lol, but they edited it out.
I find it funny most of the negative ”Experts” are from country’s where only way you can even see guns like on the show are in a museum . Losers
Is me but is her husband a retard
Agreed … he’s a huge moron.
Well, I am not at all surprised at anything stupid I see on that idiotic TV show that is so very often staged and has the MOST OBNOXIOUS Main character of any “reality” show I have ever seen. That yes does indeed give all gun enthusiasts a bad name and are the perfect representatives of the gun community for the liberals to point at and say, “See, see! See!”
And even MORE so, I am not a bit Surprised to learn the Star of the show, the “Owner of the shop”, that stupid father of hers is a two time CONVICTED CHILD MOLESTER, of BOTH his daughters when they were TWELVE Year old LITTLE GIRLS! It is obvious now that he’s as much a perv sicko as he is an overzealous attention starved horrible actor that exemplifies the insult people mean when they call someone a “Gun Nut”. In this one show he has set us proud gun owners back YEARS in our quest to be understood as normal, good, honest and well respected people… Unlike the inbred looking”Macho” acting personality of the now known pervert Will Hayden. What an obnoxious Macho tool he has always been and I hope they keep him in prison forever just so the world won’t have to look at his self righteous mug and idiotic personality that has always been the complete opposite and wrong representation of what most common gun enthusiasts in America are really like…..The OPPOSITE of HIM.
So I say give the poor girl a break, while yes she gets the “bad acting” award of the decade and does costar in one of the worst shows ever, I give her a pass for having grown up under such an idiotic chest pounding tool, and being molested by him to boot?!- The poor thing, no wonder she’s all bent up in the brain.